Taschenrechner

An der Matur am Gymnasium Biel-Seeland erlaubte Taschenrechnermodelle:

TI-30X IIS

TI-30 Eco Rs

Hinweis

Falls Sie an der Oberstufe einen anderen Taschenrechner verwendet haben, lohnt sich eine frühzeitige Umstellung, damit Sie sich an den neuen Taschenrechner gewöhnen können.

Übungen

RUnden auf 3 Nachkommastellen

Allen Resultate müssen auf 3 Nachkommastellen gerundet werden.

Grundlegendes

1. Aufgabe

   $$\frac{17.38 \cdot 3}{9}$$
   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   17.38*3/9

   TI-30 Eco

   17.38 * 3 ÷ 9 =

2. Aufgabe

   $$\frac{1 + 2 + (-3)^2}{3}$$
   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   (1 + 2 + 3²)/3

   TI-30 Eco

   ( 1 + 2 + 3 x² ) ÷ 3 =

   Rechenregeln

   • $(-3)^2 = -3 \cdot -3$, da "Minus mal Minus" Plus ergibt, kann der Ausdruck direkt als 3² eingegeben werden.
   • Soll dennoch das -3 explizit eingegeben werden, muss es in Klammern stehen (1 + 2 + (-3)²)/3.

3. Aufgabe

   $$\frac{2}{3}\cdot\frac{2.2}{7.3}\cdot \frac{8.1}{2.7} \cdot 4$$
   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   2 / 3 * 2.2 / 7.3 * 8.1 / 2.7 * 4

   TI-30 Eco

   2 ÷ 3 * 2.2 ÷ 7.3 * 8.1 ÷ 2.7 * 4 =

   Rechenregeln

   • Es kann auch 2 * 2.2 * 8.1 * 4 / 3 / 7.3 / 2.7 eingegeben werden, da reine Punktoperationen kommutativ sind.

4. Aufgabe

   $$\frac{7-\sqrt{7^2-4\cdot 2 \cdot (-4)}}{2\cdot 2}$$
   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   (7 - √(7² + 4*2*4))/4

   TI-30 Eco

   ( 7 - ( 7 x² + 4 * 2 * 4 ) √x ) ÷ 4 =

   Vereinfachungen

   • Simple Dinge wie $2\cdot 2$ (oder eigentlich auch $7^2$) können im Kopf berechnet und direkt eingegeben werden.
   • Im Radikand wird $+4\cdot 2\cdot 4$ anstatt $-4 \cdot 2 \cdot (-4)$ eingegeben, da ein Produkt mit einer geraden Anzahl negativer Terme immer positiv wird.
   • Den Taschenrechner brauchen wird, damit wir schneller sind - solche Vereinfachungen helfen, weniger Tasten einzugeben und weniger Fehler zu machen.

5. Aufgabe

   $$\frac{-(-8)-\sqrt{(-8)^2-4\cdot 2.378 \cdot 4}}{2\cdot 2.378}$$
   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   (8 - √(8² - 4 * 2.378 * 4)) / 2 / 2.378

   oder alternativ

   (8 - √(8² - 4 * 2.378 * 4)) / (2 * 2.378)

   TI-30 Eco

   ( 8 - ( 8 x² - 4 * 2.378 * 4 ) √x ) ÷ 2 ÷ 2.378 =

   oder alternativ

   ( 8 - ( 8 x² - 4 * 2.378 * 4 ) √x ) ÷ ( 2 * 2.378 ) =

   Vereinfachungen

   • Ein Produkt im Nenner kann auch als mehrmaliges Teilen eingegeben werden: $\frac{6}{2\cdot 3}=6\cdot \frac{1}{2} \cdot \frac{1}{3} = 6 ÷ 2 ÷ 3 = 1$.

Platonische Körper

Es gibt genau $5$ platonische Körper, sog. reguläre Polyeder.

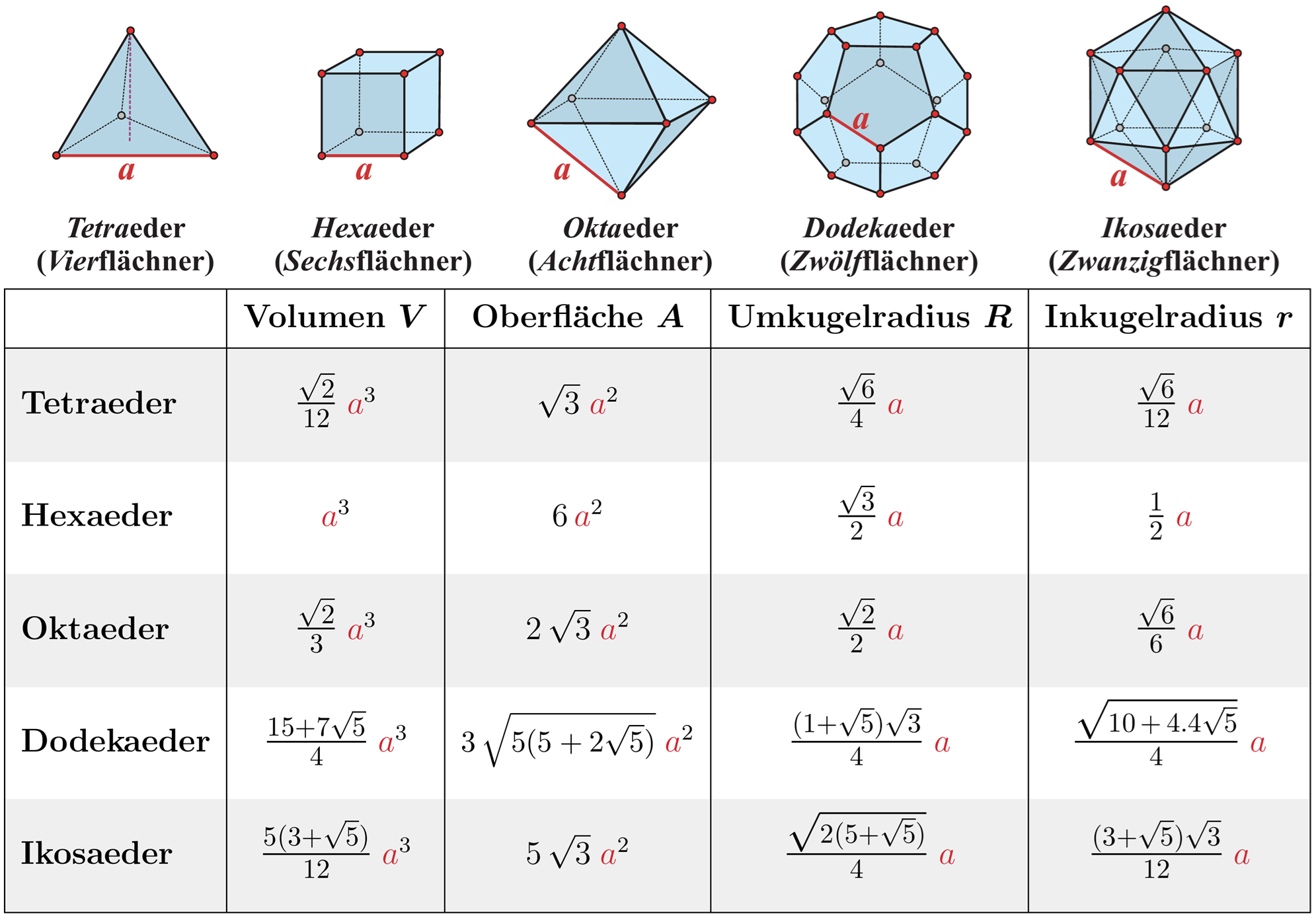Formelsammlung Mathematik, A. Wetzel, S. 13

1. Berechnen Sie die Oberfläche eines Dodekaeders mit der angegebenen Kantenlänge und runden Sie das Ergebnis auf 3 Nachkommastellen genau.

   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   3√(5*(5+2√(5)))*25²

   Optimierung

   Zwischen Faktoren und Wurzeln muss nicht zwingend ein * stehen.

   TI-30 Eco

   Von Innen- nach Aussen die Klammern berechnen.

   3 * ( 5 * ( 5 + 2 * 5 √x ) ) √x * 25 x² =

   Alternativ ohne Klammern (hier möglich, da Zwischenresultate als Faktoren verwendet werden): 5 √x + 5 = * 5 = √x * 3 * 25 x² =

   Gleich-Taste

   Die Gleich-Taste = berechnet das Resultat - sie soll nur dann verwendet werden, wenn

   • eine Rechnung abegschlossen ist
   • das gesamte bisher Eingegeben als Faktor verwendet werden soll
   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   Wurde bereits das Resultat für $25\, cm$ berechnet, kann mit der Taste die letzte Eingabe abgerufen und die Kantenlänge auf $75\, cm$ geändert werden.

   Optimierung

   Steht das Resultat bereits auf dem Display, kann auch mit direkt ans Ende der letzten Rechnung gesprungen werden.

   TI-30 Eco

   Nochmals alles eingeben...

   3 * ( 5 * ( 5 + 2 * 5 √x ) ) √x * 75 x² =

2. Berechnen Sie das Volumen eines Ikosaeders auf 3 Nachkommastellen genau:

   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   5*(3+√5)/12*17^3

   TI-30 Eco

   5 * ( 3 + 5 √x ) ÷ 12 * 17 yˣ 3 =

   Laden...

Dezimalzahlen zu Brüchen

Umwandeln von Dezimalzahlen in Brüche

Dezimalzahlen können von Taschenrechnern zu ganzzahligen Brüchen umgeformt werden.

$$0.333\overline{3} = \frac{1}{3}$$

Beispiel

$\frac{215}{1505}$ soll gekürzt und als Bruch dargestellt werden.

Wobei die Taste wie folgt einzugeben ist:

TI-30X IIS

215 ÷ 1505 F ◀▶ D

Wobei F ◀▶ D = 2nd PRB

TI-30 Eco

215 ÷ 1505 F ◀▶ D

Wobei F ◀▶ D = 2nd

Abkürzung F ◀▶ D

Die Abkürzung F ◀▶ D steht für die Umwandlung von einem Bruch in eine Dezimalzahl und bei erneuter Anwednung umgekehrt.

F

Fraction [Bruch]

D

Decimal [Dezimalzahl]

Gemeine Brüche (falls Zähler > Nenner)

Gemeine Brüche (auch unechte Brüche) können vom TR nicht dargestellt werden. Sie werden als ganze Zahl + Stammbruch dargestellt:

$$\frac{8}{3} = 2\frac{2}{3}$$

TI-30X IIS

2 ⊔ 2/3

TI-30 Eco

2_2⯾3

Der Bruch muss also händisch erweitert werden.

Schreiben Sie als gemeinen Bruch. Eingabe als Zähler/Nenner, bspw. $\frac{8}{3}$ als 8/3.

1. Aufgabe

   Laden...

2. Aufgabe

   $$\frac{708}{3^2\cdot 4 \cdot 7}$$
   Laden...

   Vorgehen und Tipps

   708 / (9 * 4 * 7) F ◀▶ D

   ergibt 2 ⊔ 17/21. Zähler: 2 * 21 + 17 = 59 Nenner: 21

Trigonometrische Funktionen

1. Aufgabe: Wie gross ist der gesuchte Winkel, wenn im rechtwinkligen Dreieck die Ankathete $a=3$ und die Gegenkathete $b=7$ beträgt?

   Laden...

2. Aufgabe: Schreiben Sie die Lösung als Bruch. (Winkel in Radiant)

   Laden...

   Vorgehen und Tipps

   Den Taschenrechner auf RAD stellen.

   $$sin^{-1}(0.5) = 0.523598776$$

   Dies ist nicht wirklich eine anschauliche Zahl. Weil wir aber mit RAD rechnen und dort eine $360^{\circ}$ Drehung $2\pi$ entsprechen, können wir versuchen, die Zahl als Vielfaches oder als Bruch von $\pi$ darzustellen. Am einfachsten Teilt man die Zahl durch $\pi$ und entscheidet, ob die entstehende Zahl als Bruch geschrieben werden kann.

   $$\begin{align*} \frac{0.523598776}{\pi} &= 0.1666\overline{6} = \frac{1}{6} \qquad \qquad | \cdot \pi \\ \rightarrow \qquad \frac{1}{6} \cdot \pi &= 0.523598776 \end{align*}$$

   und somit $\frac{\pi}{6}$ (in die Lösung eingeben als pi / 6).

3. Aufgabe: Schreiben Sie die Lösung als Bruch. (Winkel in Radiant)

   Laden...

Zwischenresultate abspeichern

Auf dem Taschenrechner können Zwischenresultate abgespeichert werden. Dies ist besonders nützlich, wenn ein Resultat mehrmals verwendet wird, oder (nur für den TI-30X) falls eine Formel für mehrere Parameter berechnet werden soll.

TI-30X IIS

Abspeichern

STO ▶ A|B|C|D|E =

Abrufen

MEMVAR A|B|C|D|E =

TI-30 Eco Rs

Abspeichern

STO Taste 1|2|3 (oben links steht dann M1, M2 oder M3)

Abrufen

RCL Taste 1|2|3

Ungerundete Zwischenresultate

Zwischenresultate dürfen nicht gerundet werden, da sich der Rundungsfehler sonst im Verlauf der weiteren Rechnung signifikant auf das Endresultat auswirken kann. Zwischenresultate können aber gespeichert werden und damit weitergerechnet werden.

Übung: Schiefer Wurf

Um herauszufinden, wie weit ein Ball maximal fliegt (ohne Beachtung des Luftwiederstands und ohne Miteinbezug der Abwurfhöhe), kann folgende Formel benutzt werden:

$$\textbf{Weite} w = \frac{v^2 \cdot sin(2\alpha)}{g}$$

Wobei $g=9.81$ die Erdanziehungskraft und $v$ die Abwurfgeschwindigkeit des Balles in $\frac{m}{s}$ ist.

Wie weit fliegt ein Ball, der im $30^{\circ}$ Winkel mit einer Geschwindigkeit von $50\frac{km}{h}$ geworfen wird? (Zwischenresultat im TR abspeichern).

Laden...

Laden...

Übung: Kreissegment

Im Formelbuch findet man folgende Formel für Flächenberechnungen im Kreis:

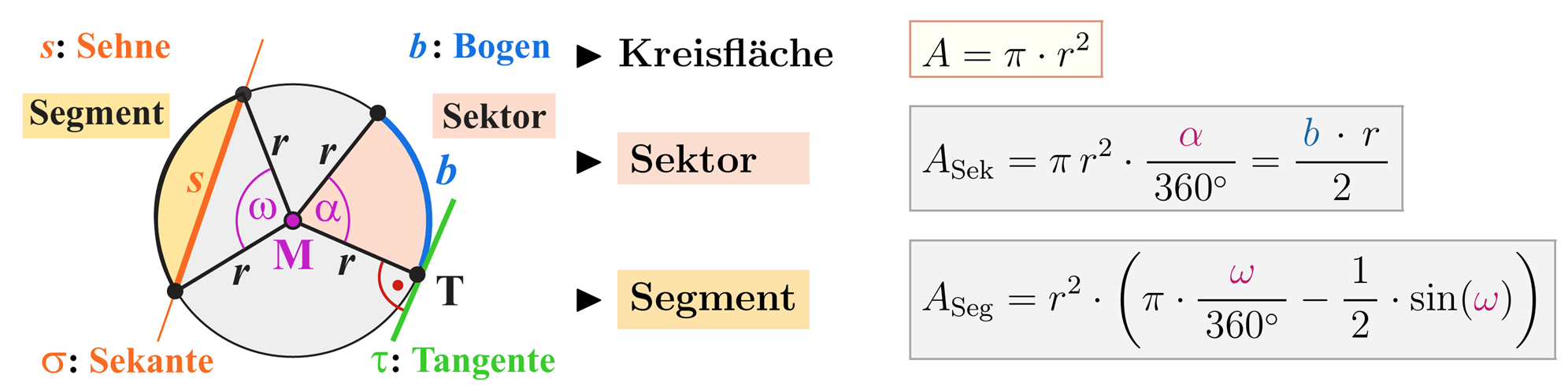Formelsammlung Mathematik, A. Wetzel, S. 9

Berechnen Sie für einen Kreis mit Radius $23\,cm$ die Fläche des Kreissegmentes, wenn der Winkel:

1. $30^{\circ}$ beträgt.

   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   23² * (π * 30 / 360 - sin(30) / 2)

   TI-30 Eco

   23 ² * ( π * 30 ÷ 360 - 30 sin ÷ 2 ) =

2. $35^{\circ}$ beträgt.

   Laden...

   ⚠️ Vorgehen und Tipps

   TI-30X IIS

   1. Mit 35 STO ▶ = die $35^{\circ}$ als A abspeichern.
   2. Mit 2x▲ die Formel aus der ersten Aufgabe hervorholen und alle $30$ mit A ersetzen (löschen kann man mit DEL).:

   23² * (π * A / 360 - sin(A) / 2)

   3. jetzt sind alle weiteren Aufgaben leicht: die gesuchte Winkelangabe als A abspeichern und die Formel ausführen.

   TI-30 Eco

   Leider gibts keine entsprechende Vereinfachung wie beim TI-30X. Die Formel muss also jedes Mal neu eingegeben werden.

3. $40.2^{\circ}$ beträgt.

   Laden...

4. $45.1234^{\circ}$ beträgt.

   Laden...

   Vorgehen und Tipps

   TI-30X IIS

   So weiter wie bisher - Tipp von Aufgabe 2 beachten.

   TI-30 Eco

   Damit die Zahl $45.1234$ nicht mehrfach eingegeben werden muss, kann sie auch abgespeichert werden und dann mit RCL wieder abgerufen werden.

   45.1234 STO 1 (Zahl speichern)

   23 ² * ( π * RCL 1 ÷ 360 - RCL 1 sin ÷ 2 ) =

5. $55.122333444455555^{\circ}$ beträgt.

   Laden...